Рис.1. Проектные чертежи храма Александра Невского, выполненные архитектором К.Лыгиным.

На сегодняшний день он имеет статус памятника истории и культуры регионального значения, который играет важную роль в формировании облика города Новосибирска являясь одним из важнейших символов города.

Прототипом форм храма предположительно послужил одноименный храм Александра Невского, построенный в Тифлисе (Тбилиси) по проекту академика архитектуры Давида Ивановича Гримма [1]. Тифлисский прототип был разрушен большевиками в 1930-м году. Поэтому о его формах можно судить только по сохранившимся фотографиям (Рис.2).

Рис.2. Храм Александра Невского в Тифлисе

Новониколаевский храм после Октябрьского переворота много лет пустовал. С 1957 по 1985 гг. здание занимала Западно-Сибирская студия кинохроники, в 1985 г. оно передается Новосибирской филармонии с целью размещения в нем камерного хора. 25 августа 1989 г. принято решение о передаче здания храма Новосибирской Епархии.

В 1980- е годы, в рамках проведения реставрационных работ, было проведено большое научно-историческое исследование памятника [2]. Однако, в архитектуроведческом отношении формы храм остаются до сих пор еще недостаточно изученными. В частности, совершенно не изучены его пропорционально-метрологические особенности, которые, теоретически, могут дать ключ к пониманию логики формообразования.

Для проведения пропорционально-метрологического исследования необходимо наличие детальных обмерных чертежей. В период реставрации здания храма в 80-х годах прошлого столетия были сделаны достаточно подробные обмерные чертежи, фиксирующие существующее положение форм памятника (рис.3).

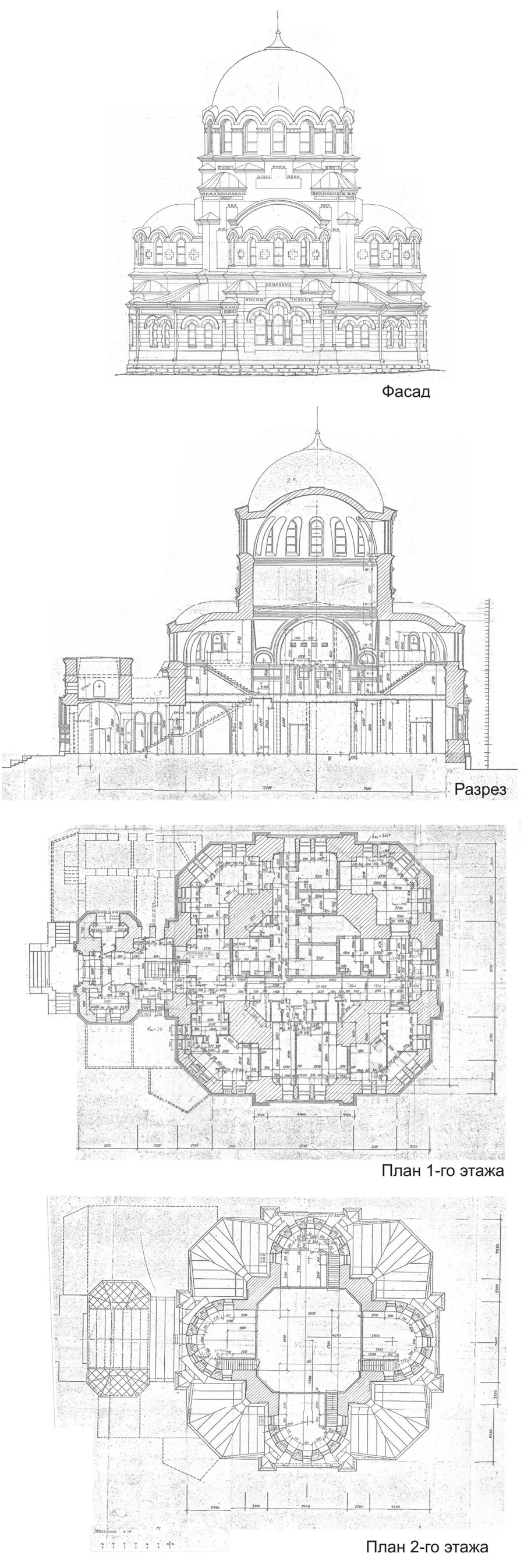
Рис. 3. Обмерные чертежи, выполненные традиционным способом в период реставрации храма А.Невского в 1980-е годы.

В настоящее время появилась возможность повторить обмерную фиксацию форм на несоизмеримо более высоком технологическом уровне с помощью технологии объемного лазерного сканирования, которая позволяет зафиксировать размеры и формы исследуемого памятника архитектуры с максимально возможной полнотой. Если раньше уходили недели, а иногда и месяцы, на то, чтобы произвести обмеры всего объекта [3], то в настоящее время с использованием современных технологий работу можно выполнить в очень короткий срок. В частности, на сканирование форм храма Александра Невского ушло 3–4 часа. В России данная технология активно применяется в Санкт-Петербурге (фирма «Фотограмметрия»). Для выполнения обмеров фасадов здания используется разработанная ими технология, сочетающая методы лазерного сканирования и цветовой фотограмметрии [4]. Также существует зарубежный опыт, который можно изучить в отчете по сканированию форм римского Пантеона [5].

Благодаря совместной работе с Региональным Центром лазерного сканирования, действующем при Сибирской государственной геодезической академии нам представилась возможность изучить данную технологию и получить максимально полную обмерную информацию по формам храма Александра Невского. Доступными для измерения стали буквально все, «видимые» лучом лазера, точки объекта. Было получено так называемое «облако точек» (объемом файла составил примерно 8 гигабайт). Это облако точек, условно говоря, было «нарезано» на отдельные слои как по вертикали – по осям Х и Y, так и по горизонтали – оси Z (рис.4).

.

Рис.4. Слои из облака точек по осях Х, и Z.

Слои по оси Z, в которых наиболее четко просматривается форма объекта, были переведены из облаков точек в векторную форму в виде чертежей, выполненных в программе AutoCAD (рис.5).

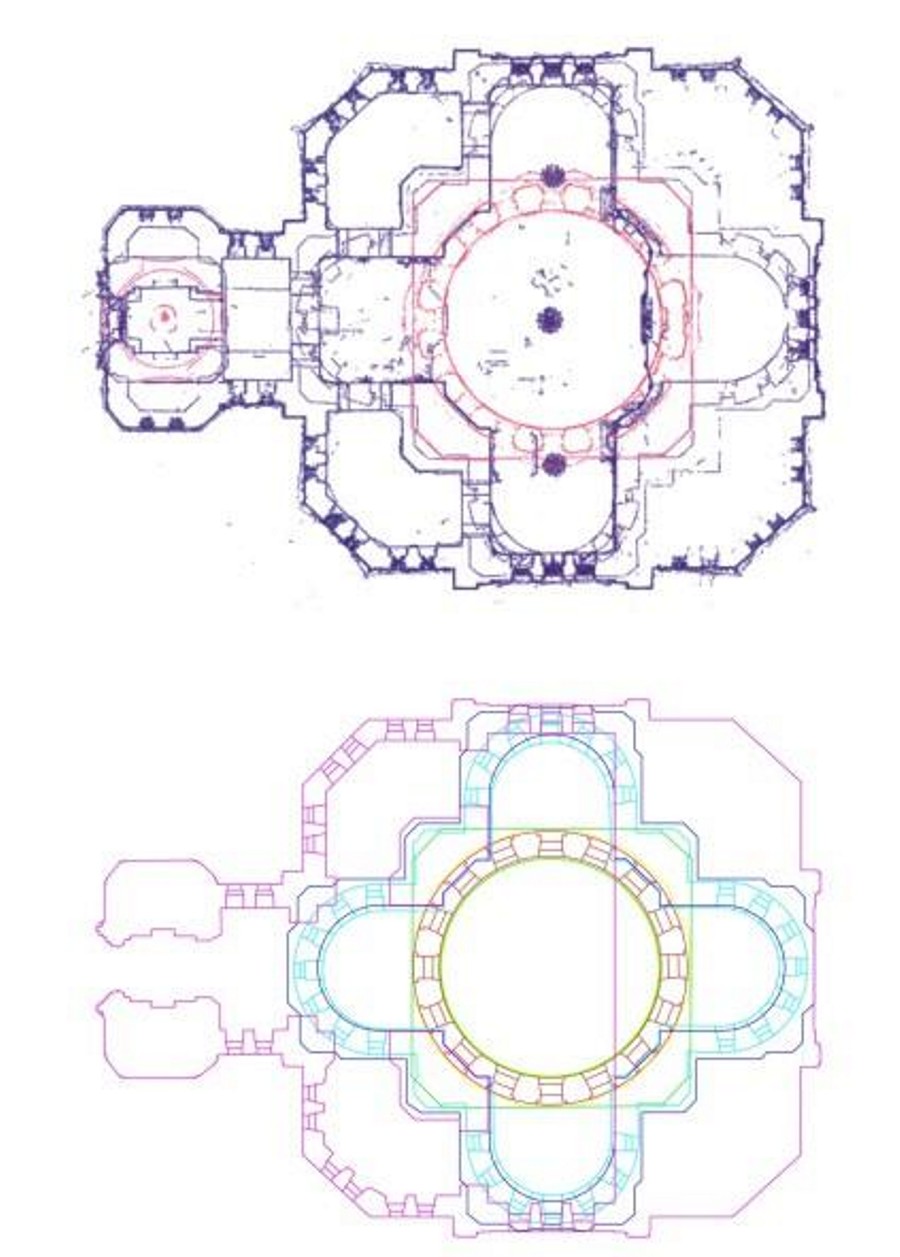
Рис.5. Планы полученные из облака точек (сверху) в линейный вид (снизу).

Полученные таким образом чертежи отличаются высокой степенью деталировки и точностью измерения (Рис.6).

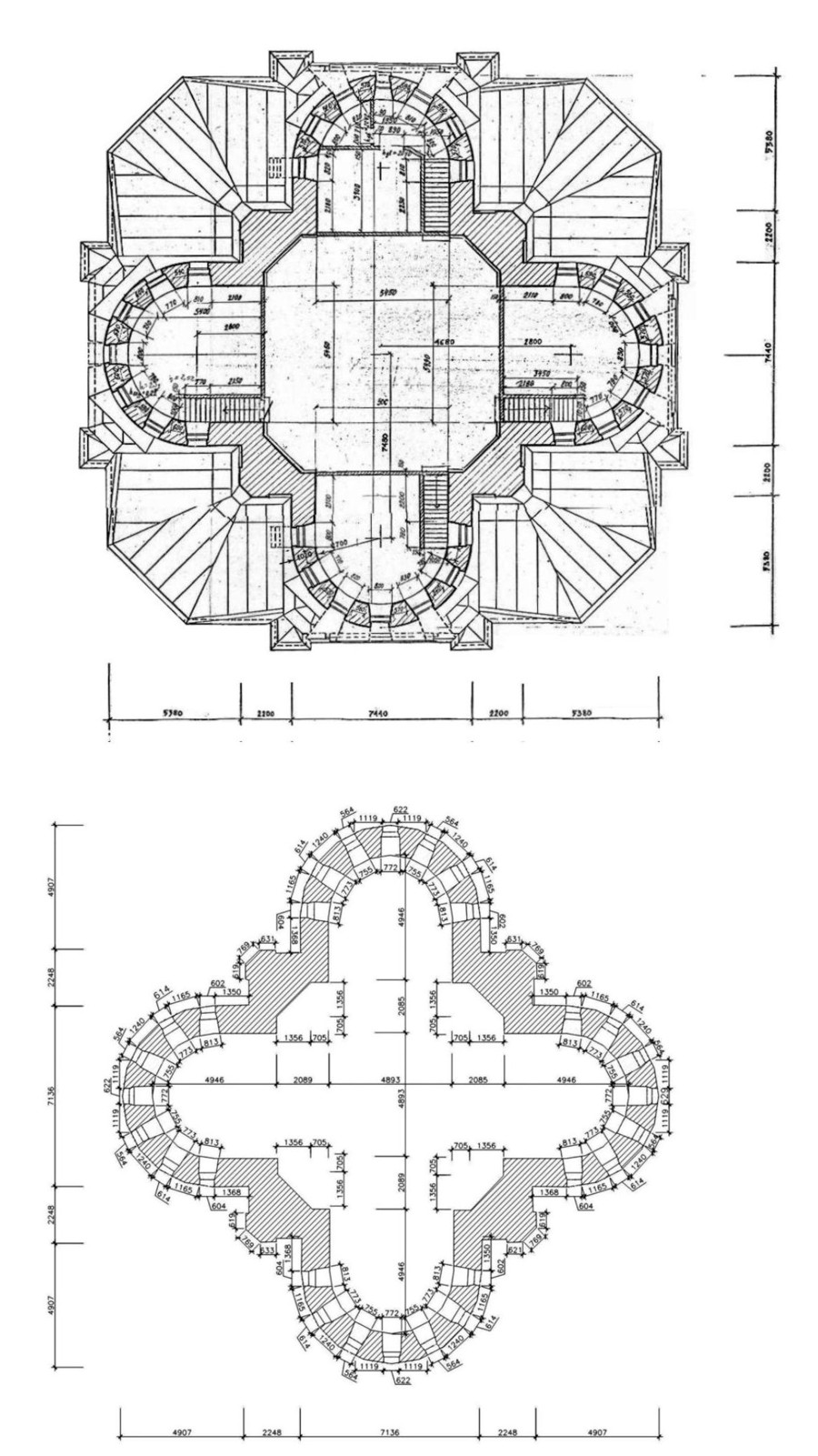
Рис. 6. Сопоставление чертежей выполненных по результатам ручной (сверху) и лазерной фиксации (снизу).

Автоматизация процессов измерений и выполнения чертежей дает возможность производить несоизмеримо более качественную и подробную фиксацию форм архитектурных объектов. Очевидно, что через некоторое время технология такой фиксации станет стандартной для документирования во многих направлениях реставрационно-проектной деятельности.

Наряду с попыткой освоения новой технологии обмеров, нами также была осуществлена попытка провести научный анализ полученных размеров и пропорций, с целью выявления логики формообразования.

Методика исследования [6] в идеале, предполагает наличие следующих материалов:

               1. Авторские чертежи с обозначением размеров;

               2. Обмерные чертежи;

               3. Точное знание, используемых при проектировании, стандартов мер длины.

В нашем случае присутствуют все, необходимые для исследования, материалы. Есть проектные чертежи К.Лыгина на которых присутствует масштабная линейка в саженях (рис.7).

Рис.7. Проектные чертежи архитектора К.Лыгина с выделением

масштабной линейки.

Есть также точные обмеры, произведенные с помощью объемного лазерного сканирования. Технология такого сканирования позволяет получать практически любые двухмерные чертежи с объекта. Пример такого «чертежа» набранного из множества точек, «вырезанных» в определенной плоскости из общего облака точек, приведен на рис. 8. Такой чертеж позволяет увидеть даже изменение геометрии стен барабана, что явилось следствием распора от тяжести купола. Измерения показывают, что верхний диаметр барабана примерно на 10 сантиметров больше нижнего. Зафиксировать такую деформацию с помощью обычных «ручных» обмеров практически невозможно.

Рис.8. Продольный разрез храма А.Невского, полученный путем

«среза» из облака точек.

Сопоставление обмеров и проектных чертежей (Рис. 9) может дать важную информацию для исследования объекта. Наложение чертежей друг на друга дало возможность выявить целый ряд особенностей отличающих проектный замысел от существующего положения. Во-первых, видно, что в проекте К.Лыгина отсутствует уровень хор. По всей видимости хоры были сконструированы в результате реконструкции храма в 1980-е годы. Во-вторых, видно, что уровень щелыги подпружных арок имеет значительное различие. По нашим замерам, их проектная высота от уровня пола составляет 16 аршин, а в реальном объекте она равна 15 аршинам. Можно предположить, что проектный замысел был откорректирован еще во время выполнения строительных работ. В-третьих, сопоставление чертежей показывает большое различие в очертаниях колокольни. В связи с тем, что колокольня храма была разрушена большевиками, ее пришлось реставрировать заново. Выявленные различия говорят о том, что реставрация была произведена весьма произвольно.

Рис.9. Сопоставление проектного чертежа с обмерами.

Дальнейшее исследование основывается на переводе размеров из современной метрической системы мер в старорусские меры — сажени (2,13м), аршины (0,71м), вершки (0,044м). Используя эти меры можно попытаться реконструировать некоторые особенности исходного проектного замысла. Проанализируем основные размеры фасада и разреза, запроектированных архитектором К.Лыгиным (рис.10).

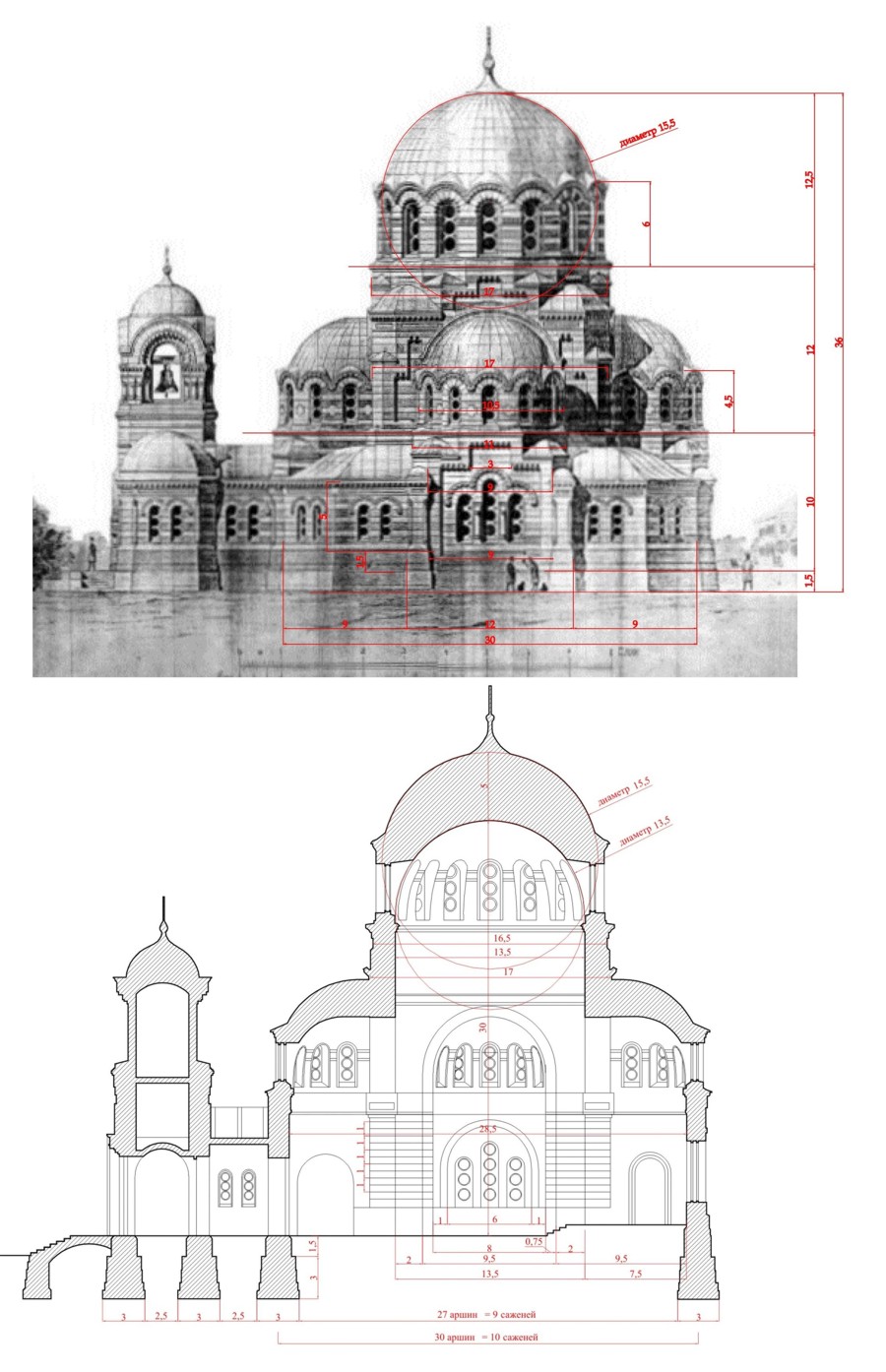
 Рис.10. Метрологический анализ форм храма А.Невского (размеры приведены в аршинах).

Проведенный нами метрологический анализ дал возможность выявить некоторые метрические особенности форм собора. Так, например, можно зафиксировать метрическую закономерность в построении фасадной части здания. Онаимеет трехчастное деление: центральная часть составляет 12 аршин, а две боковые — по 9 аршин. Следовательно, полная ширина фасада получается равной 30 аршинам или 10 саженям. По вертикальным размерам можно отметить, внутренняя высота храма равна 30 аршинам или 10 саженям. На середине этого размера расположены щелыги подпружных арок (по лазерному обмеру — 10,60м).

Восстановление проектных размеров храма, теоретически, может дать основания для проведения гипотетической реконструкции исходного проектного замысла. Если использовать в качестве модуля толщину стен барабана и боковых экседр, равную 1,065 м, что составляет четыре кирпича или половину сажени (1,5 аршина), то можно заметить, что в основании плана лежит окружность с диаметром 9 модулей и примыкающими к нему с четырех сторон окружностями диаметром 5 модулей (Рис. 11). Все остальные горизонтальные размеры храма, по всей видимости, были производными от этой геометрической схемы.

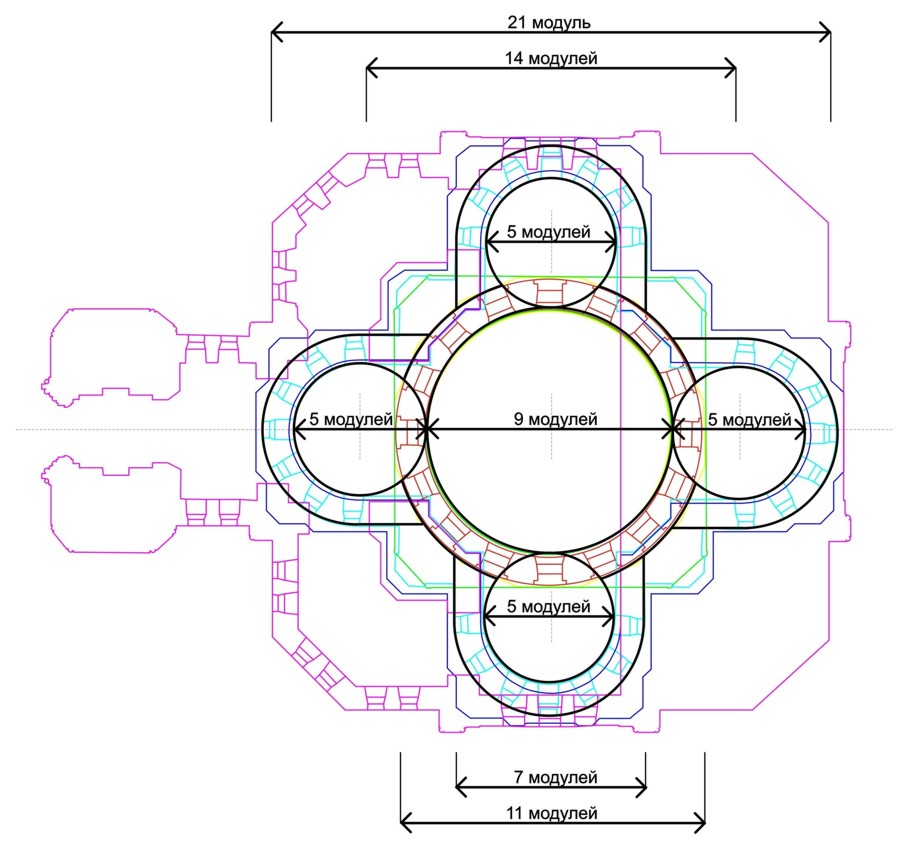
Рис.11. Анализ плана храма А.Невского.

Более полная реконструкция проектной логики Собора, безусловно, требует дальнейшего исследования. Кроме того, для полноты картины необходимо проведение подобных исследований по как можно большему количеству подобных объектов.

Тем не менее, проведенное исследование дает возможность утверждать, что архитектор К.Лыгин использовал при проектировании храма Александра Невского простые модульные соотношения на основе аршина и сажени. В основе логики формообразования плана лежит геометрическая схема, состоящая из пяти окружностей: одной центральной и примыкающих к ней с четырех сторон окружностей меньшего диаметра.

Список литературы:

1. Радзюкевич А.В. К вопросу об авторстве и прототипах собора Св. Александра Невского в Новониколаевске (Новосибирске)

http//www.a3d.ru/architecture/stat/190

1. Собор Александра Невского в Новосибирске. Проект реставрации фасадов. Историческая справка. Архив НПЦ по сохранению историко-культурного наследия.

2. Соколова Т.Н., Рудская Л.А., Соколов А.Л. Архитектурные обмеры. М. 2007.

3. http//www.photogrammetria.ru

4. http//www.digitalpantheon.ch/repository

5. Радзюкевич А.В. Методические основы проведения пропорционально-метрологического анализа форм памятников архитектуры. Дисс. на соик. уч. ст. канд. арх. Новосибирск. 2004.